 FRIENDS OF THE TURTLE
FRIENDS OF THE TURTLEDavid D Thornburg, Associate Editor
The
Logo Kaleidoscope
One of the first programming projects for many BASIC programmers is the construction of a screen kaleidoscope that generates pretty, symmetrical patterns on the display screen. For these programs, people usually pick a screen location at random and then place a colored dot at that location and at three other "mirror" locations to produce four symmetrically placed dots. While the resulting image is often quite attractive, the result is not that of a true kaleidoscope.
If you have ever taken a kaleidoscope apart, you must have wondered how such a simple apparatus could generate such beautiful images. Most kaleidoscopes consist of a set of mirrors and some small pieces of colored plastic that can be shaken to take random positions on a flat surface. When you look through the eyepiece, the mirrors generate multiple images of the arrangement of plastic pieces to produce beautifully symmetric pictures. Because Logo's turtle graphics allows you to easily create images that imitate the pieces of plastic, it is possible to create quite attractive kaleidoscopic images on your computer screen with a simple set of procedures.
The Logo kaleidoscope operates in the following manner. The system contains a set of graphic procedures to draw the fundamental picture elements (squares, triangles, stars, etc.). There can be as many of these elements as you desire (subject to the memory limitations of your system, of course). Each of these elements can be drawn as large as you desire. This gives the effect of having even more patterns to choose from.
Next, we use Logo's random number generator to select a shape, a size for the shape, the shape's color, and a distance from the center of the screen at which the shape will be drawn. Finally, this data is used by another procedure that places a copy of the chosen shape at several equally spaced angles around the center of the screen. Once one shape has been drawn, the process can be repeated for other shapes until the final image meets with your approval.
The kaleidoscope we will demonstrate in this article is written in the MIT version of Logo for the Apple II and should work with most Logo systems with very few modifications..
The kaleidoscope was started out with six shapes.
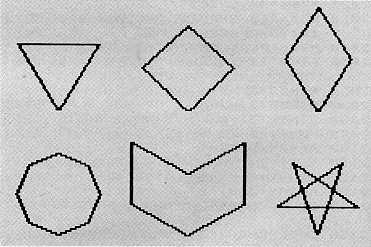
The procedures for these shapes are:
TO
TRI :SIZE
LT 30
REPEAT 3 [FD :SIZE RT 120]
RT 30
END
TO DIAMOND :SIZE
LT 45
REPEAT 4 [FD :SIZE RT 90]
RT 45
END
TO PATT1 :SIZE
LT 30
REPEAT 2 [FD :SIZE RT 60 FD :SIZE RT 120]
RT 30
END
TO OCT :SIZE
LT 67.5
REPEAT 8 [FD :SIZE/2 RT 45]
RT 67.5
END
TO PATT2 :SIZE
LT 60
FD :SIZE RT 60 FD :SIZE RT 120
FD :SIZE LT 60 FD :SIZE RT 120
FD :SIZE RT 60 FD :SIZE RT 120
END
TO STAR :SIZE
LT 18
REPEAT 5 [FD :SIZE RT 144]
RT 18
END
LT 30
REPEAT 3 [FD :SIZE RT 120]
RT 30
END
TO DIAMOND :SIZE
LT 45
REPEAT 4 [FD :SIZE RT 90]
RT 45
END
TO PATT1 :SIZE
LT 30
REPEAT 2 [FD :SIZE RT 60 FD :SIZE RT 120]
RT 30
END
TO OCT :SIZE
LT 67.5
REPEAT 8 [FD :SIZE/2 RT 45]
RT 67.5
END
TO PATT2 :SIZE
LT 60
FD :SIZE RT 60 FD :SIZE RT 120
FD :SIZE LT 60 FD :SIZE RT 120
FD :SIZE RT 60 FD :SIZE RT 120
END
TO STAR :SIZE
LT 18
REPEAT 5 [FD :SIZE RT 144]
RT 18
END
Each of these figures has been defined to have mirror symmetry on the vertical axis. This is not a requirement, and you may wish to experiment with other orientations. The octagon was drawn at half the specified size to keep it in balance with the other figures.
Constructing The Pattern
To make the kaleidoscopic image, we need a procedure that creates a list of basic patterns, chooses a pattern at random from this list, and selects an appropriate size (say between 20 and 50 units). Next, it should pick a random distance from the center (less than 60 units, to keep the images on the screen). Once these steps have been completed, copies of the chosen image should be stamped symmetrically around the screen. Then the procedure should wait for you to tell it if you want another element added to the image. When you press the RETURN key, the process will be repeated. The following procedure performs these tasks for us:
TO
IMAGE
MAKE "LIST [STAR DIAMOND OCT PATT1
PATT2 TRI]
MAKE "NAME SENTENCE PICKRANDOM :LIST
(20 + RANDOM 30)
MAKE "DIST RANDOM 60
PENCOLOR (1 + RANDOM 5)
PENUP
WINDMILL :DIST :NAME
MAKE "NAME REQUEST
IMAGE
END
MAKE "LIST [STAR DIAMOND OCT PATT1
PATT2 TRI]
MAKE "NAME SENTENCE PICKRANDOM :LIST
(20 + RANDOM 30)
MAKE "DIST RANDOM 60
PENCOLOR (1 + RANDOM 5)
PENUP
WINDMILL :DIST :NAME
MAKE "NAME REQUEST
IMAGE
END
This procedure uses two other procedures that have to be defined: PICKRANDOM and WINDMILL. The function of PICKRANDOM is to choose an element of a list randomly. The following procedure does this for us:
TO
PICKRANDOM :LIST
OUTPUT PICK (1 + RANDOM (LENGTH :LIST))
:LIST
END
OUTPUT PICK (1 + RANDOM (LENGTH :LIST))
:LIST
END
The procedure PICK selects a given element from a list, and LENGTH measures the number of elements in a list:
TO
PICK :NUM :LIST
IF :NUM = 1 OUTPUT FIRST :LIST
OUTPUT PICK (:NUM -1) (BUTFIRST :LIST )
END
TO LENGTH :LIST
IF :LIST = [] THEN OUTPUT 0
OUTPUT 1 + LENGTH BUTFIRST :LIST
END
IF :NUM = 1 OUTPUT FIRST :LIST
OUTPUT PICK (:NUM -1) (BUTFIRST :LIST )
END
TO LENGTH :LIST
IF :LIST = [] THEN OUTPUT 0
OUTPUT 1 + LENGTH BUTFIRST :LIST
END
These two procedures operate "recursively." If you have a hard time understanding how they work, you may want to read about them in Logo for the Apple II, by H. Abelson, or read the chapter on recursion in my book Discovering Apple Logo. Also, we published some columns on recursion in "Friends of the Turtle" (COMPUTE!, November and December 1982).
Defining Windmill
The only procedure we have left to define is WINDMILL. The function of this procedure is to draw a chosen pattern at equally spaced angular increments around the center of the screen. You may want to experiment with different numbers of images. I have tried using six images spaced at 60-degree increments and eight images spaced at 45-degree increments. These both work fine, but other angles are worth exploring as well. The number of copies of a pattern times the angle increment must be 360 in order for the pattern to be symmetric. That is why we turn 60 degrees for 6 copies (6 x 60 = 360) and 45 degrees for 8 copies (8 x 45 = 360).
TO
WINDMILL :DIST :LIST
REPEAT 6 [FD :DIST PENDOWN RUN :LIST
PENUP BACK :DIST RT 60]
END
REPEAT 6 [FD :DIST PENDOWN RUN :LIST
PENUP BACK :DIST RT 60]
END
To generate a kaleidoscopic pattern, hide the turtle and enter:
IMAGE
After the first pattern is drawn, press RETURN to get the next one. When the complexity of the pattern is satisfactory, you may want to print a copy of it or save it on your disk (with SAVEPICT, for example). If you are ambitious, you might want to write a Logo procedure that will keep track of all the randomly chosen values and generate its own Logo procedures for each pattern. Abelson's book (mentioned above) shows how to do this sort of thing.
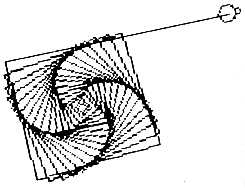
The following five pictures show the successive development of one pattern:

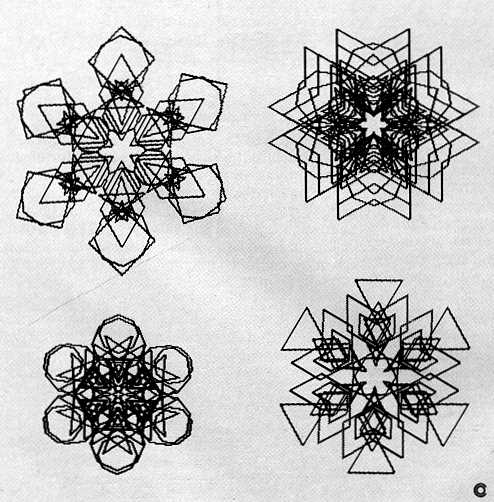
The remaining figures illustrate some other kaleidoscopic patterns that were generated with this set of procedures.
I think you will agree that these patterns are more interesting than those created with colored dots.